Reduce kernel in CUDA
cuda basics techTable of Contents
Question definition
Given an array of \(n\) integers, the goal is to compute the sum of all elements within the array.
Solutions
The implementations for all kernel versions can be found at 2-reduce.cu on GitHub.
Naive Version with atomicAdd
The simplest approach involves utilizing each thread to perform an atomicAdd operation on the output variable. Here’s how the kernel is defined:
__global__ void reduce_naive_atomic(int* g_idata, int* g_odata, unsigned int n)
{
unsigned int idx = blockIdx.x * blockDim.x + threadIdx.x;
unsigned int gridSize = blockDim.x * gridDim.x;
int sum = 0;
for (unsigned int i = idx; i < n; i += gridSize)
{
sum += g_idata[i];
}
atomicAdd(g_odata, sum);
}
And the kernel launcher is straightforward, invoking the kernel a single time:
int launch_reduce(int* g_idata, int* g_odata, unsigned int n, int block_size, kernel_fn kernel, cudaStream_t stream)
{
int* idata = g_idata;
int* odata = g_odata;
uint32_t num_warps = block_size / 32;
int smem_size = num_warps * sizeof(int);
int num_blocks = ceil(n, block_size);
// Launch the kernel
kernel<<<num_blocks, block_size, smem_size, stream>>>(idata, odata, n);
if (!FLAGS_profile)
cudaStreamSynchronize(stream);
// Copy the final result back to the host
int h_out;
NVCHECK(cudaMemcpyAsync(&h_out, odata, sizeof(int), cudaMemcpyDeviceToHost, stream));
return h_out;
}
When tested on a GTX 4080, this method achieved a throughput of approximately 82GB/s.
Tiled Reduction with Shared Memory
A classical approach involves leveraging a thread block to perform local reductions on a tile within shared memory. This method encompasses several kernel versions, each with different optimizations.
Basic version
The initial implementation is as below:
- A tile of data is collaboratively loaded into shared memory.
- A partial reduction on this data tile is executed within a thread block, get the sum of the tile.
- The sum is then written to a designated spot in the global memory’s output slot. It’s important to note that this kernel requires a temporary buffer for writing partial results from each thread block.
- The process repeats with the size \(n\) reduced to \(\frac{n}{blockSize}\), continuing until \(n=1\).
__global__ void reduce_smem_naive(int* g_idata, int* g_odata, unsigned int n)
{
extern __shared__ int sdata[];
unsigned int tid = threadIdx.x;
unsigned int i = blockIdx.x * blockDim.x + threadIdx.x;
// Read a block of data into shared memory collectively
sdata[tid] = (i < n) ? g_idata[i] : 0;
__syncthreads();
for (unsigned int stride = 1; stride < blockDim.x; stride *= 2)
{
// ISSUE: divergent warps
if (tid % (2 * stride) == 0)
{
sdata[tid] += sdata[tid + stride];
}
__syncthreads(); // need to sync per level
}
// Write the result for this block to global memory
if (tid == 0)
{
g_odata[blockIdx.x] = sdata[0];
}
}
Launching this kernel multiple times involves a slightly more complex launcher:
int launch_reduce(int* g_idata, int* g_odata, unsigned int n, int block_size, kernel_fn kernel, cudaStream_t stream,
uint32_t num_blocks, uint32_t smem_size)
{
int* idata = g_idata;
int* odata = g_odata;
if (smem_size == 0)
smem_size = block_size * sizeof(int);
// Calculate the number of blocks
num_blocks = (num_blocks > 0) ? num_blocks : (n + block_size - 1) / block_size;
if (!FLAGS_profile)
printf("- launching: num_blocks: %d, block_size:%d, n:%d\n", num_blocks, block_size, n);
int level = 0;
// Launch the kernel
kernel<<<num_blocks, block_size, smem_size, stream>>>(idata, odata, n);
if (!FLAGS_profile)
cudaStreamSynchronize(stream);
level++;
// Recursively reduce the partial sums
while (num_blocks > 1)
{
std::swap(idata, odata);
n = num_blocks;
num_blocks = (n + block_size - 1) / block_size;
kernel<<<num_blocks, block_size, smem_size, stream>>>(idata, odata, n);
if (!FLAGS_profile)
cudaStreamSynchronize(stream);
}
// Copy the final result back to the host
int h_out;
NVCHECK(cudaMemcpyAsync(&h_out, odata, sizeof(int), cudaMemcpyDeviceToHost, stream));
return h_out;
}
All tiled reduction kenrels utilize the aforementioned launcher, achieving a throughput of 54GB/s. This is less efficient compared to the atomic naive version, which reaches 82GB/s.
Avoid thread divergence
The basic version encounters significant thread divergence, particularly noticeable at if (tid % (2 * stride) == 0).
Here is an optimized variant:
__global__ void reduce_smem_1_avoid_divergent_warps(int* g_idata, int* g_odata, unsigned int n)
{
extern __shared__ int sdata[];
unsigned int tid = threadIdx.x;
unsigned int i = blockIdx.x * blockDim.x + threadIdx.x;
sdata[tid] = (i < n) ? g_idata[i] : 0;
__syncthreads();
for (unsigned int stride = 1; stride < blockDim.x; stride *= 2)
{
int index = 2 * stride * tid;
if (index < blockDim.x)
{
// Issue: bank conflict
sdata[index] += sdata[index + stride];
}
__syncthreads();
}
if (tid == 0)
{
g_odata[blockIdx.x] = sdata[0];
}
}
The optimization yields a 70GB/s throughput, marking a 29% improvement over the basic version.
Read two elements one time
The preceding version’s DRAM throughput was only 20.63%, likely due to
- Insufficient grid size for small inputs, leading to underutilized thread resources.
- Each thread reading a single element at a time, given the fixed number of resident thread blocks per SM for a specific kernel, results in a limited number of load instructions issued.
To enhance DRAM throughput, especially for smaller grid sizes, threads can be configured to read more than one element at a time.
__global__ void reduce_smem_3_read_two(int* g_idata, int* g_odata, unsigned int n)
{
extern __shared__ int sdata[];
unsigned int tid = threadIdx.x;
unsigned int i = blockIdx.x * (blockDim.x * 2) + threadIdx.x;
#define GET_ELEM(__idx) ((__idx) < n ? g_idata[(__idx)] : 0)
sdata[tid] = GET_ELEM(i) + GET_ELEM(i + blockDim.x);
__syncthreads();
for (unsigned int stride = 1; stride < blockDim.x; stride *= 2)
{
int index = 2 * stride * tid;
if (index < blockDim.x)
{
// Issue: bank conflict
sdata[index] += sdata[index + stride];
}
__syncthreads();
}
if (tid == 0)
{
g_odata[blockIdx.x] = sdata[0];
}
}
This approach improves the DRAM Throughput to 33.78%, a significant 63.72% increase over the previous method. The overall throughput reaches 96.51GB/s, demonstrating 37.87% enhancement from the 70GB/s achieved earlier.
Tiled Reduction with Warp Shuffle
Modern GPUs facilitate direct data exchange within a warp, bypassing the need for shared memory.
The function below demonstrates how to conduct a reduction within a single warp using the warp shuffle instruction, as highlighted in the book <Professional CUDA C Programming>.
// using warp shuffle instruction
// From book <Professional CUDA C Programming>
__inline__ __device__ int warpReduce(int mySum)
{
mySum += __shfl_xor(mySum, 16);
mySum += __shfl_xor(mySum, 8);
mySum += __shfl_xor(mySum, 4);
mySum += __shfl_xor(mySum, 2);
mySum += __shfl_xor(mySum, 1);
return mySum;
}
Utilizing shared memory to store the sum computed by each warp and subsequently reducing these sums as previously described enables the calculation of a thread block’s total sum.
__global__ void reduce_warp_shlf(int* g_idata, int* g_odata, unsigned int n)
{
// Helps to share data between warps
// size should be (blockDim.x / warpSize)
extern __shared__ int sdata[];
unsigned int idx = blockIdx.x * blockDim.x + threadIdx.x;
// Necessary to make sure shfl instruction is not used with uninitialized data
int mySum = idx < n ? g_idata[idx] : 0;
int lane = threadIdx.x % warpSize;
int warp = threadIdx.x / warpSize;
mySum = warpReduce(mySum);
if (lane == 0)
{
sdata[warp] = mySum;
}
__syncthreads();
// last warp reduce
mySum = (threadIdx.x < blockDim.x / warpSize) ? sdata[lane] : 0;
if (warp == 0)
{
mySum = warpReduce(mySum);
}
if (threadIdx.x == 0)
{
g_odata[blockIdx.x] = mySum;
}
}
Despite reading only a single element per thread, this kernel can achieve a throughput of 96GB/s, outperforming the shared memory version’s 70GB/s. Furthermore, the kernel can be modified to read \(NT\) elements at a time for enhanced efficiency:
template <int NT>
__global__ void reduce_warp_shlf_read_N(int* g_idata, int* g_odata, unsigned int n)
{
// Helps to share data between warps
// size should be (blockDim.x / warpSize)
extern __shared__ int sdata[];
int blockSize = NT * blockDim.x;
unsigned int idx = blockIdx.x * blockSize + threadIdx.x;
// Necessary to make sure shfl instruction is not used with uninitialized data
#define GET_ELEM(__idx) ((__idx) < n ? g_idata[(__idx)] : 0)
int mySum = 0;
#pragma unroll
for (int i = 0; i < NT; i++)
mySum += GET_ELEM(idx + i * blockDim.x);
int lane = threadIdx.x % warpSize;
int warp = threadIdx.x / warpSize;
mySum = warpReduce(mySum);
if (lane == 0)
{
sdata[warp] = mySum;
}
__syncthreads();
// last warp reduce
mySum = (threadIdx.x < blockDim.x / warpSize) ? sdata[lane] : 0;
if (warp == 0)
{
mySum = warpReduce(mySum);
}
if (threadIdx.x == 0)
{
g_odata[blockIdx.x] = mySum;
}
}
Performance varies with different \(N\) values, as summarized below:
| NT | throughput (GB/s) |
|---|---|
| 1 | 96.3187 |
| 2 | 96.2341 |
| 4 | 96.8153 |
| 8 | 107.226 |
Warp Shuffle Combined with Atomic Operations
Compared to tiled reduction solutions, utilizing atomicAdd eliminates the need for a temporary buffer and requires only a single kernel launch.
This segment explores combining warp shuffle and atomic operations for efficient reduction.
The kernel template below demonstrates this approach, utilizing warp shuffle instructions to enhance the warp reduction performance, and leveraging atomic operations to write directly to the output slot without the need for temporary buffer and multiple kernel launches.
template <int NT>
__global__ void reduce_warp_shlf_read_N_atomic(int* g_idata, int* g_odata, unsigned int n)
{
// Helps to share data between warps
// size should be (blockDim.x / warpSize)
extern __shared__ int sdata[];
int blockSize = NT * blockDim.x;
unsigned int idx = blockIdx.x * blockSize + threadIdx.x;
// Necessary to make sure shfl instruction is not used with uninitialized data
// This only needs one turn of launch
#define GET_ELEM(__idx) ((__idx) < n ? g_idata[(__idx)] : 0)
int mySum = 0;
#pragma unroll
for (int i = 0; i < NT; i++)
mySum += GET_ELEM(idx + i * blockDim.x);
int lane = threadIdx.x % warpSize;
int warp = threadIdx.x / warpSize;
mySum = warpReduce(mySum);
if (lane == 0)
{
sdata[warp] = mySum;
}
__syncthreads();
// last warp reduce
mySum = (threadIdx.x < blockDim.x / warpSize) ? sdata[lane] : 0;
if (warp == 0)
{
mySum = warpReduce(mySum);
}
if (threadIdx.x == 0)
{
atomicAdd(g_odata, mySum);
}
}
Remarkably, this kernel achieves a throughput of 121.777 GB/s under the same conditions.
Benchmark
The benchmark results illustrate the performance of different CUDA optimization strategies under varying conditions.
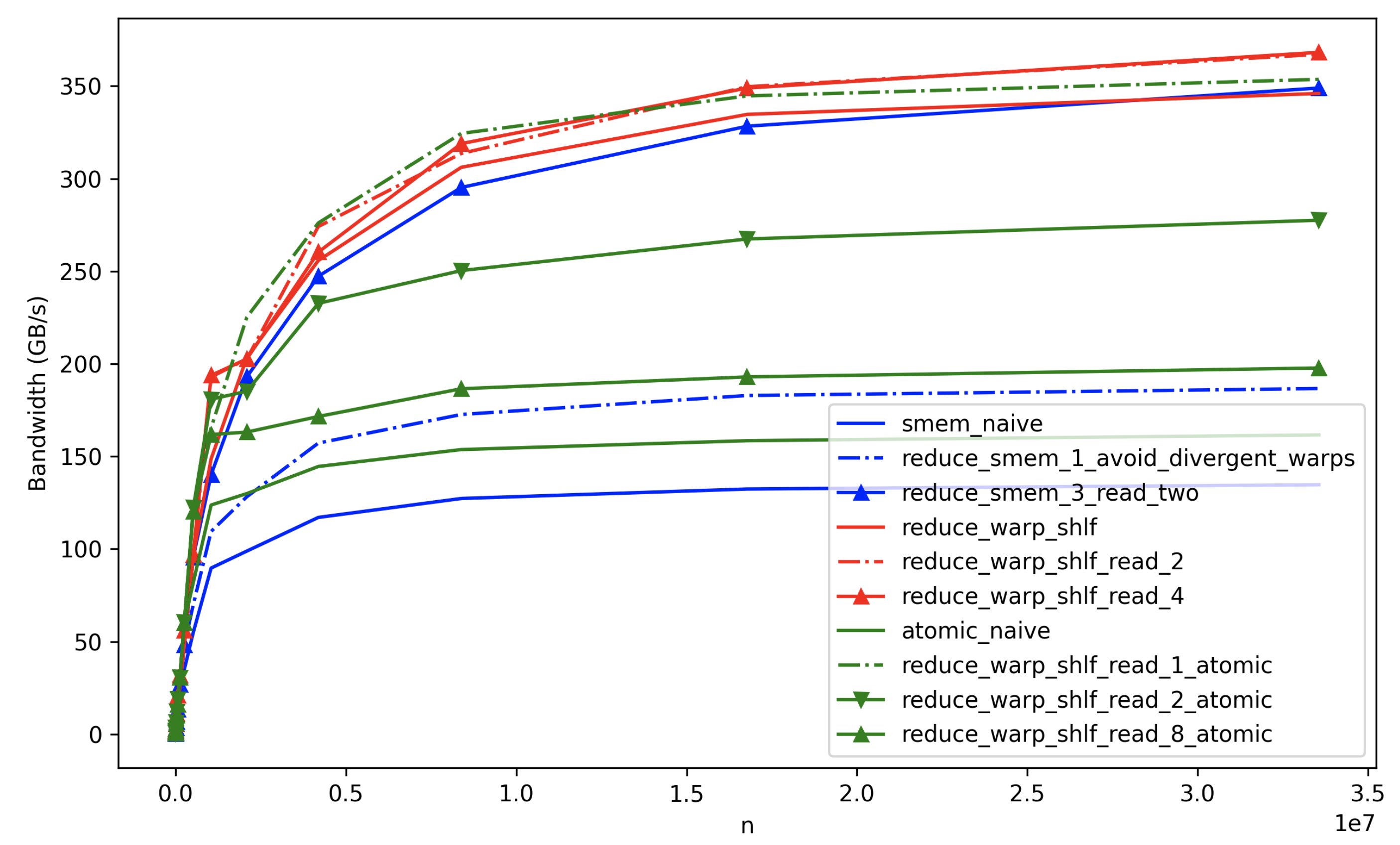
Note that the optimal kernel configuration may vary depending on the size of the input data(\(n\)).