OpenAI/Triton MLIR 迁移工作简介

Nov 15, 2022 triton system tech

Table of Contents

经过几个月的不懈努力，OpenAI Triton已经成功完成了面向MLIR Infra的迁移/重构工作，并将其最新的基于MLIR的代码合并至主分支。这个工作是由OpenAI和NVIDIA相关团队近几个月来深入合作完成的，而我也有幸参与其中。在这篇文章中，我将分享一些技术总结，记录一些收获和思考。

尽管Triton目前的开源开发非常迅速，但本文将主要聚焦于基于MLIR Infra进行重构的第一个版本的代码（这应该也是两三个月前的）

Triton 简介

OpenAI Triton paper 中的介绍是 “An Intermediate Language and Compiler for Tiled Neural Network Computations”，其中几个关键词应该能够代表其特点：

Intermediate Language, 目前是基于 Python 的 DSL
Compiler ，是一个经典的 Compiler 的架构
Tiled Computation，面向 GPU 体系特点，自动分析和实施 tiling

定位

由于 Triton 的开发非常迅速，这里只讨论当前 Triton 的功能。

简而言之，Triton 提供了一套针对 GPU Kernel 的开发的 Language（基于 Python）和高性能 Compiler。

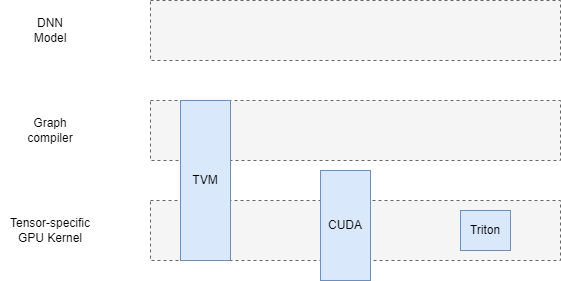
因此，就层次而言，Triton的 DNN 开发能力与 CUDA 的部分相对应，但与TVM、XLA等直接面向 DL 的 Domain compiler 无法完全对应。后者更像是面向 DL 的武器库，拥有从构图到 auto fusion 等端到端的能力，而Triton则更像一把小巧、实用的瑞士军刀，面向偏底层的也是最通用的 Kernel 开发问题。

新代码中的架构

Triton 新代码中的架构总体上可以如下呈现

即总体上可以分为三大块

Frontend，将用户的 Python kernel code 转换为 Triton IR，以及维护 kernel launch 的 Runtime
Optimizer，通过各类 pass 将 Triton IR 逐步转换为优化过的 TritonGPU IR
Backend，将 TritonGPU IR 逐步转换为 LLVM IR，并最终通过 ptxas 编译为 cubin

贯穿这三部分的核心表示是 Triton 的 IR，微观上，IR 也分为两个层次

Triton Dialect，表示计算逻辑，硬件无关的表达
TritonGPU Dialect，GPU 相关的计算表示

这两者都是基于 MLIR 的自定义 dialect，除此之外，Triton 也复用了很多社区的 dialect 来进行宏观的表示，包括

std dialect： tensor, int, float 等数据类型
arith dialect：各类数学操作
scf dialect：if, for 等控制流
nvvm dialect：获取 thread_id 等少量操作
gpu dialect：printf 等少量操作

下图是 Triton 中核心表示完整的转换过程：

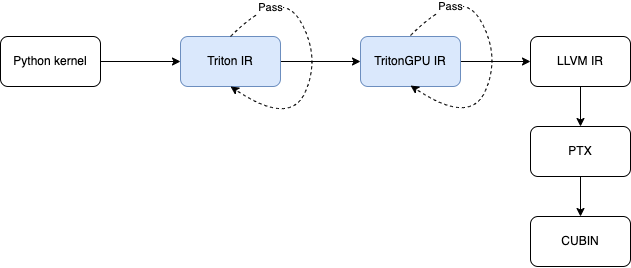
其中蓝色的两部分主要是 MLIR 体系涉及的部分，随后 MLIR 会转换为 LLVM IR，之后 Triton 会调用 NVPTX 转换为 PTX Assembly，随后由 CUDA 的 ptxas 编译器编译为 cubin。

Python 界面之 Frontend

Frontend 用于将用户用 Python 编写的 kernel 转换为对应的 Triton IR (Triton Dialect)，这里由于篇幅不便展开，细节可以阅读 compiler.py::CodeGenerator 中基于 Python ast 的规则。

比如 vector add 的例子

@triton.jit
def add_kernel(x_ptr, y_ptr, output_ptr, N,
               BLOCK_SIZE: tl.constexpr):
    pid = tl.program_id(0)
    block_start = pid * BLOCK_SIZE
    offsets = block_start + tl.arange(0, BLOCK_SIZE)
    mask = offsets < N
    x = tl.load(x_ptr + offsets, mask=mask)
    y = tl.load(y_ptr + offsets, mask=mask)
    output = x + y
    tl.store(output_ptr+offsets, output, mask=mask)

# x, y are torch.Tensor
grid = lambda meta: (triton.cdiv(n_elements, meta['BLOCK_SIZE']),)
add_kernel[grid](x, y, output, n_elements, BLOCK_SIZE=1024)

相应会得到 Triton IR

func public @kernel_0d1d2d3d(
       %arg0: !tt.ptr<f32> {tt.divisibility = 16 : i32},
       %arg1: !tt.ptr<f32> {tt.divisibility = 16 : i32},
       %arg2: !tt.ptr<f32> {tt.divisibility = 16 : i32},
       %arg3: i32 {tt.divisibility = 16 : i32}) {
  %c256_i32 = arith.constant 256 : i32
  %0 = tt.get_program_id {axis = 0 : i32} : i32
  %1 = arith.muli %0, %c256_i32 : i32
  %2 = tt.make_range {end = 256 : i32, start = 0 : i32} : tensor<256xi32>
  %3 = tt.splat %1 : (i32) -> tensor<256xi32>
  %4 = arith.addi %3, %2 : tensor<256xi32>
  %5 = tt.splat %arg0 : (!tt.ptr<f32>) -> tensor<256x!tt.ptr<f32>>
  %6 = tt.addptr %5, %4 : tensor<256x!tt.ptr<f32>>
  %7 = tt.splat %arg1 : (!tt.ptr<f32>) -> tensor<256x!tt.ptr<f32>>
  %8 = tt.addptr %7, %4 : tensor<256x!tt.ptr<f32>>
  %9 = tt.splat %arg3 : (i32) -> tensor<256xi32>
  %10 = arith.cmpi slt, %4, %9 : tensor<256xi32>
  %11 = tt.load %6, %10
  %12 = tt.load %8, %10
  %13 = arith.addf %11, %12 : tensor<256xf32>
  %14 = tt.splat %arg2 : (!tt.ptr<f32>) -> tensor<256x!tt.ptr<f32>>
  %15 = tt.addptr %14, %4 : tensor<256x!tt.ptr<f32>>
  tt.store %15, %13, %10 : tensor<256xf32>
  return
}

可以看到，Triton IR 几乎一比一地对应到原始的 Python code，将用户定义的 computation 带入 MLIR 的体系，后续会在此基础上做各类优化（by Optimizer）以及最终 translate 到更低层次的表示中（by Backend）。

性能优化之 Optimizer

Optimizer 用于分析和优化 Frontend 传入的 IR，通过各类 Transformation 和 Conversion (Pass) 策略，最终传递给 Backend 做 translate。

Optimizer 大致的 workflow 如下

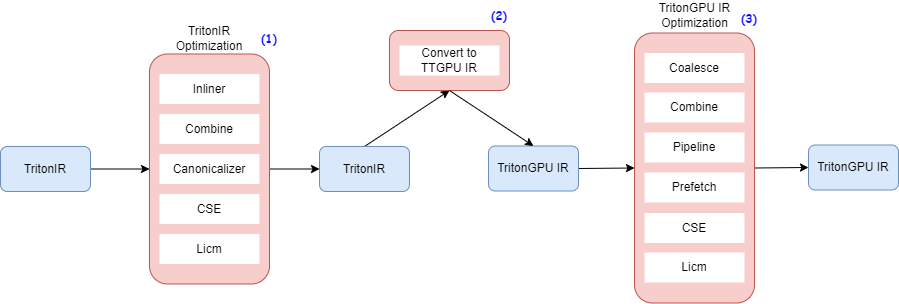
主要分为三大块优化

TritonIR 的优化
TritonIR to TritonGPU IR 的 Conversion
TritonGPU IR 的优化

贯穿中间的数据结构是 TritonGPU IR，顾名思义是带上了 GPU 相关的信息的 IR。

TritonGPU Dialect

TritonGPU Dialect 相比 Triton Dialect，主要是增加了 GPU 硬件相关的 Op 和 Type。

Data layout

Data layout 是 TritonGPU Dialect 的 Type system 的关键，确定了 Data(各层级memory中的Tensor) 到 thread 之间的映射关系。

目前 Triton 中有如下几种

Blocked Layout

Blocked Layout 表示 thread 间平均分配 workload 的情况，每个线程 own 一块 memory 上连续的 data 进行处理。

其包含了如下三个字段用于帮助确定 thread 和数据之间的映射关系：

sizePerThread：每个 thread 处理的 连续排布 的元素数目
threadsPerWarp：每个 Warp 在不同维度上的线程数，用向量表示
warpsPerCTA：每个 CTA 对应的 Warp 数目，这个由用户在 Python 层制定

按代码中的例子

For example, a row-major coalesced layout may partition a 16x16 tensor over 2 warps (i.e. 64 threads) as follows.

[ 0  0  1  1  2  2  3  3  ; 32 32 33 33 34 34 35 35 ]
[ 0  0  1  1  2  2  3  3  ; 32 32 33 33 34 34 35 35 ]
[ 4  4  5  5  6  6  7  7  ; 36 36 37 37 38 38 39 39 ]
[ 4  4  5  5  6  6  7  7  ; 36 36 37 37 38 38 39 39 ]
...
[ 28 28 29 29 30 30 31 31 ; 60 60 61 61 62 62 63 63 ]
[ 28 28 29 29 30 30 31 31 ; 60 60 61 61 62 62 63 63 ]

for

#triton_gpu.blocked_layout<{
  sizePerThread = {2, 2}
  threadsPerWarp = {8, 4}
  warpsPerCTA = {1, 2}
}>

Shared Layout

Shared Layout：表示数据在 shared memory 的一些特性，比如 swizzle 访问的一些参数。

其包含了如下字段

vec, 支持 vectorization 的单位
perPhase, 每个 phase 包含多少个 vec
maxPhase, tensor 总共包含多少个 phase
order, axis 的次序

其中，vec, perPhase, maxPhase 是用于避免 bank conflict 的 swizzle 操作需要的参数。

代码中的例子：

In order to avoid shared memory bank conflicts, elements may be swizzled
in memory. For example, a swizzled row-major layout could store its data
as follows:

A_{0, 0}  A_{0, 1}  A_{0, 2}  A_{0, 3} ...   [phase 0] \ per_phase = 2
A_{1, 0}  A_{1, 1}  A_{1, 2}  A_{1, 3} ...   [phase 0] /
groups of vec=2 elements
are stored contiguously
_ _ _ _ /\_ _ _ _
A_{2, 2}  A_{2, 3}  A_{2, 0}  A_{2, 1} ...   [phase 1] \ per phase = 2
A_{3, 2}  A_{3, 3}  A_{3, 0}  A_{3, 1} ...   [phase 1] /

1. MMA Layout
顾名思义，MMA Layout 表示 Tensor Core 中 MMA 指令结果的 data layout，比如 Ampere 对应的 MMA Layout 的数据排布基本可以对应到 PTX 指令中的 mma.m16n8k16 的 C,D 的排布。
MMA Layout 主要包含两个字段：
- version ，表示 TensorCore 的版本
  - 1 为 Volta
  - 2 为 Ampere
- warpsPerCTA
这里演示 FP16 精度下， version=2 的数据排布（会映射到 mma.m16n8k16 指令）的 Accumulators (C or D) 的数据排布。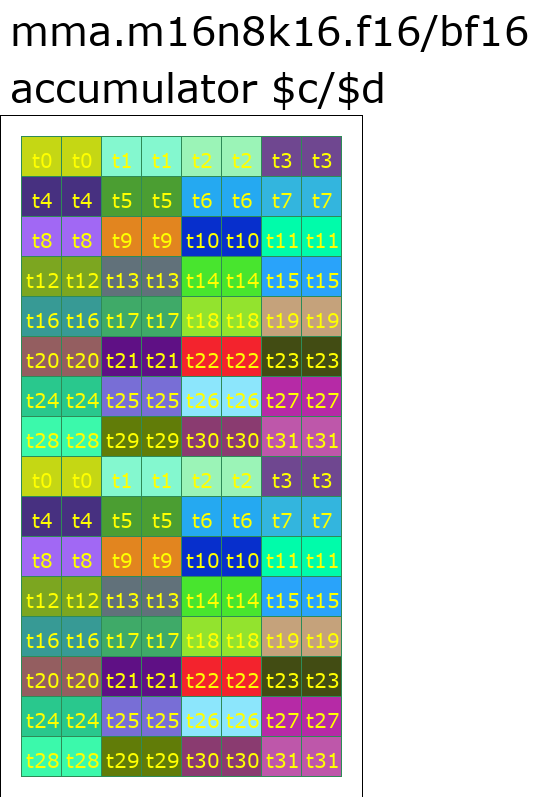

1. DotOperand Layout
DotOperand Layout 用来表示 Triton 的 DotOp 的输入的 layout。
其主要包含如下信息
1. opIdx ， Operand 的 ID
  - opIdx=0 表示 DotOp 的 $a
  - opIdx=1 表示 DotOp 的 $b
2. parent ，存储其对应的 MMA Layout，这里 DotOperand 的数据排布也可能间接的由 MMA Layout 确定（如果 DotOp lower 到 MMA 指令）或者 Blocked Layout（如果 DotOp lower 到 FMA 指令）
这里为了方便演示，我们采用 MMA Layout 中的 mma.m16n8k16.f16 指令
- 计算精度为 FP16
- MMA Layout
  - version=2
  - warpsPerCTA=[8,4]
- 对于 $a，对应的 DotOperand 的 opIdx = 0
- $b, 对应的 DotOperand 的 opIdx = 1

1. Slice Layout
Slice Layout 表明单个维度上的数据反向索引

ConvertLayoutOp

顾名思义，ConvertLayoutOp 就是用来讲 Tensor 从一种 data layout 转换到另外一种 data layout。由于 data layout 是 TensorType 的一部分，很自然会存在类型（其中layout）需要转换的情况，这就是 ConvertLayoutOp 的作用。

有了上面的 Data Layout，接下来我们看最简单的 MatMul 中的的 IR：

#blocked0 = #triton_gpu.blocked<{sizePerThread = [1, 8], threadsPerWarp = [16, 2], warpsPerCTA = [1, 1], order = [1, 0]}>
#blocked1 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [4, 8], warpsPerCTA = [1, 1], order = [1, 0]}>
#mma = #triton_gpu.mma<{version = 2, warpsPerCTA = [1, 1]}>

// ...
%37 = tt.load %arg8 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16xf16, #blocked0>
%38 = tt.load %arg9 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8xf16, #blocked1>
%39 = triton_gpu.convert_layout %37 : (tensor<16x16xf16, #blocked0>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>
%40 = triton_gpu.convert_layout %38 : (tensor<16x8xf16, #blocked1>) -> tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>
%41 = tt.dot %39, %40, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>> * tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>> -> tensor<16x8xf32, #mma>
// ...

上面是截取了一段经典 MatMul 中某个阶段的 TritonGPU IR，逻辑比较直白，定义了 #blocked0, #blocked1 和 #mma 三种 layout，之后通过 tt.load 将 DotOp 的两个 Operand 从 GEMM 加载数据到 register files，之后两个 triton_gpu.convert_layout 转换 layout 为 DotOp 的参数需要的 #triton_gpu.dot_op layout。

这里列举一些典型的 data layout 的转换，以及特点：

#shared -> #blocked ，正常是代表数据从 shared memory 被 load 到 register file 中，需要考虑 swizzle
#blocked -> #shared ，代表数据从 register file 存储到 shared memory 中，需要上一步相同的 swizzle 方式
#mma -> #blocked ，正常是 DotOp 的输出转换为更简单的 layout 来进一步计算，由于涉及到跨 thread 间的数据传递，因此一般会借由 shared memory 中转一次
#blocked -> #dot_operand ，转换为 DotOp 的输入，这一步可能也需要 shared memory 中转

Triton 中几乎实现了任意 data layout 间的转换，当然不同的转换代价也不尽相同（考虑到是否会用到 shared memory，register 增减量等等），因此转换的代价也会在 Optimizer 里面一并考虑。

TritonIR 的优化

TritonIR 上的优化主要是计算本身的，与硬件无关的优化，包含了如下 Pass

Inliner Pass，将 Kernel Call 的子函数 Inline 展开
Combine Pass，一些特定的 Pattern rewrite，比如
- select(cond, load(ptrs, broadcast(cond), ???), other) => load(ptrs, broadcast(cond), other)
Canonicalizer Pass，一些化简的 Pattern rewrite
CSE Pass，MLIR 的 cse Pass，用于 Eliminate common sub-expressions
LICM Pass，MLIR 的 LoopInvariantCodeMotion Pass ，将循环无关的变量挪到 forloop 外面

TritonGPU IR 的优化

TritonGPU IR 上的优化在计算本身优化外，新增了 GPU 硬件相关的优化，具体的 Pass 列表如下

ConvertTritonToTritonGPU Pass，将 Triton IR 转换为 TritonGPU IR，主要是增加 TritonGPU 特有的 layout
Coalesce Pass，重排 order，使得最大 contiguity 的维度排在最前面
Combine Pass，同 Triton IR
Pipeline Pass，MMA 指令对应的 global memory 到 shared memory 的 N-Buffer 优化，下文详解
Prefetch Pass，MMA 指令对应的 shared memory 到 register file 的 N-Buffer 优化，下文详解
Canonicalizer，同 Triton IR
CSE Pass，同 Triton IR
LICM Pass，同 Triton IR

Pipeline Pass

Pipeline Pass 和下一小节中的 Prefetch Pass 是配合关系，整体用来为 DotOp (mma 指令) 的 Operand 提供 IO 优化。

Pipeline 优化主要针对 DotOp 中 GEMM 到 SMEM 之间的数据拷贝，并自动做 Double Buffer 或者 N Buffer 的优化。

最简单的 Double buffer 的伪代码如下

A = alloc_tensor(shape=[2*16,16])
# cp.async & cp.async.commit_group
A = insert_slice_async(A, ptr0, 0)
B = alloc_tensor(shape=[2*16,8])
B = insert_slice_async(B, ptr1, 0)

A = insert_slice_async(A, ptr00, 1)
B = insert_slice_async(B, ptr11, 0)

async_wait(num=2) # cp.async.wait_group
A_slice0 = extract_slice(A, offset=(0,0,0), size=(1,16,16))
B_slice0 = extract_slice(B, offset=(0,0,0), size=(1,16,8))

for i in range(...):
    a = ldmatrix(A_slice0)
    b = ldmatrix(B_slice0)
    c = dot(a, b)

    offset = (i+1) % 2
    A = insert_slice_async(A, ptr2, offset)
    B = insert_slice_async(B, ptr3, offset)

    async_wait(num=2)
    A_slice0 = extract_slice(A, offset=(offset,0,0), size=(1,16,16))
    B_slice0 = extract_slice(B, offset=(offset,0,0), size=(1,16,8))

其中，

alloc_tensor 大致对应到 triton_gpu.alloc_tensor
insert_slice_async 对应到 triton_gpu.insert_slice_async ，表示异步地向 Tensor 中插入一个 slice，这个过程是通过 cp.async 指令实现的异步
tensor.extract_slice 表示从 Tensor 中读取一个 slice
async_wait 的语义对应到 cp.async.wait_group 指令

Prefetch Pass

Prefetch 的逻辑跟 Pipeline Pass 基本类似，也是 Double buffer 和 N Buffer 的优化，区别是其承担了 SMEM 到 register file 的数据搬运，IR 的表示方式是 triton_gpu.convert_layout %37 : (tensor<16x16xf16, #blocked0>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>> ，最终映射的核心指令是 ldmatrix 。

高性能 LLVM 生成之 Backend

Triton 的 Backend 可以有微观和宏观两个角度

微观上主要包括 TritonGPU IR -> LLVM Dialect 的过程，这里需要注意的是，LLVM Dialect 是 MLIR 体系中的一个表示，其可以进一步自动 lower 到 LLVM IR
宏观上进一步包括了 LLVM Dialect -> LLVM IR -> PTX -> cubin 等过程

这里我们只从微观角度介绍，因为宏观角度中，大部分流程可以通过 LLVM 社区或者 CUDA 的一些设施自动完成。

Triton 的 Backend 是比较经典的 MLIR 的 Lowering，主要内容就是将 TritonGPU IR 中包含的每种 Op 逐个的 OpConversion。不过为了高性能，以及保证 Codegen 产物的可控，Triton 在 LLVM 中大量插入了 PTX 的内联汇编（下文会介绍）。此外，大部分 Op 的 Lowering 都是比较规则化，下文会简要介绍 Dot 指令的 Lowering。

PTX inline asm

Triton 中使用 Inline asm 大致几个原因：

一些指令对应的操作在现有的 gpu 和 nvgpu 的 dialect 还不太完善
性能原因，比如浮点类型间的变换，一小块汇编足以；借助一个很长的 workflow 还不太可控

Triton 里面针对 Inline asm 的封装有个简单的 wrapper，类似最简单的 cp.async.wait_group 的调用

PTXBuilder ptxBuilder;
auto &asyncWaitOp = *ptxBuilder.create<>("cp.async.wait_group");
auto num = op->getAttrOfType<IntegerAttr>("num").getInt();
asyncWaitOp(ptxBuilder.newConstantOperand(num));

到稍微复杂点的 ld 的各种参数组合

auto &ld = ptxBuilder.create<>("ld")
                     ->o("volatile", op.getIsVolatile())
                     .global()
                     .o("ca", op.getCache() == triton::CacheModifier::CA)
                     .o("cg", op.getCache() == triton::CacheModifier::CG)
                     .o("L1::evict_first",
                        op.getEvict() == triton::EvictionPolicy::EVICT_FIRST)
                     .o("L1::evict_last",
                        op.getEvict() == triton::EvictionPolicy::EVICT_LAST)
                     .o("L1::cache_hint", hasL2EvictPolicy)
                     .v(nWords)
                     .b(width);

MMA 指令生成

相比于 ReduceOp 等需要跟 layout 结合的 Op 的 Lowering，DotOp 的是规则非常清晰的。

这里大致提下在 Backend，一个 Dot 的工作流涉及的阶段和 Op：

	Stage	Op	Layout
2	Load `$a`, `$b` 的 tile 到 SMEM	`triton_gpu.insert_slice_async`	`#shared`
3	从 SMEM Load 参数到 Register file	`tensor.extract_slice`	`#dot_op`
4	执行 MMA，结果会在 Registter file	`tt.dot`	`#mma`

所以直接跟 MMA 指令相关的其实只在第 4 步，其需要的 $a$, $b$ 两个参数已经通过 tensor.extract_slice 拷贝到了 Register file，直接满足了 Ampere 上的 mma 指令的需求。

在 Ampere 架构上，一个 DotOp 会映射到多个 mma 指令，下面我们以 FP16 的 mma.m16n8k16 指令为例，具体的任务设置如下

Dot 计算的 tile 的尺寸是 M=32, N=16, K=16
- 对应着 mma.m16n8k16 指令的尺寸是 M=16, N=8, K=16 ，因此一个 tile 需要在 m, n, k 方向展开 2x2x1 总共 4 个 mma.m16n8k16 指令

最终会有类似如下的代码

for (unsigned k = 0; k < numK; ++k)
      for (unsigned m = 0; m < numM; ++m)
        for (unsigned n = 0; n < numN; ++n) {
          callMMA(m, n, k);
        }

其中，numM, numN, numK 就对应着上面的 2, 2, 1。

callMMA 的代码如上文时候 InlineAsm，类似如下代码

 auto mma = builder.create("mma.sync.aligned.m8n8k4")
                     ->o(isARow ? "row" : "col")
                     .o(isBRow ? "row" : "col")
                     .o("f32.f16.f16.f32");

      mma(resOprs, AOprs, BOprs, COprs);

FYI

GEMM 在 Optimizer Pass 效果

下面列举了经典的 GEMM 在 Triton 的 Compile pipeline 里面的 IR 的变换。

Python code

def matmul_kernel(
    a_ptr, b_ptr, c_ptr,
    stride_am, stride_ak,
    stride_bk, stride_bn,
    stride_cm, stride_cn,
    M: tl.constexpr, N: tl.constexpr, K: tl.constexpr,
    BLOCK_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr,
    BLOCK_SIZE_K: tl.constexpr,
):
    offs_m = tl.arange(0, BLOCK_SIZE_M)
    offs_n = tl.arange(0, BLOCK_SIZE_N)
    offs_k = tl.arange(0, BLOCK_SIZE_K)
    a_ptrs = a_ptr + offs_m[:, None] * stride_am + offs_k[None, :] * stride_ak
    b_ptrs = b_ptr + offs_k[:, None] * stride_bk + offs_n[None, :] * stride_bn
    accumulator = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
    for k in range(0, K, BLOCK_SIZE_K):
        a = tl.load(a_ptrs)
        b = tl.load(b_ptrs)
        accumulator += tl.dot(a, b)
        a_ptrs += BLOCK_SIZE_K * stride_ak
        b_ptrs += BLOCK_SIZE_K * stride_bk

    c_ptrs = c_ptr + offs_m[:, None] * stride_cm + offs_n[None, :] * stride_cn
    tl.store(c_ptrs, accumulator)

Triton IR translated from Python AST(and after Inliner, CES … passes)

这一步算是 Python code 直接翻译到了 Triton IR.

  func public @matmul_kernel_0d1d2d3d4c56c78c(%arg0: !tt.ptr<f16> {tt.divisibility = 16 : i32}, %arg1: !tt.ptr<f16> {tt.divisibility = 16 : i32}, %arg2: !tt.ptr<f32> {tt.divisibility = 16 : i32}, %arg3: i32 {tt.divisibility = 16 : i32}, %arg4: i32, %arg5: i32) {
    %cst = arith.constant dense<0.000000e+00> : tensor<16x8xf32>
    %c0 = arith.constant 0 : index
    %c64 = arith.constant 64 : index
    %c16 = arith.constant 16 : index
    %cst_0 = arith.constant dense<16> : tensor<16x16xi32>
    %c16_i32 = arith.constant 16 : i32
    %0 = tt.make_range {end = 16 : i32, start = 0 : i32} : tensor<16xi32>
    %1 = tt.make_range {end = 8 : i32, start = 0 : i32} : tensor<8xi32>
    %2 = tt.expand_dims %0 {axis = 1 : i32} : (tensor<16xi32>) -> tensor<16x1xi32>
    %3 = tt.splat %arg3 : (i32) -> tensor<16x1xi32>
    %4 = arith.muli %2, %3 : tensor<16x1xi32>
    %5 = tt.splat %arg0 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>>
    %6 = tt.addptr %5, %4 : tensor<16x1x!tt.ptr<f16>>
    %7 = tt.expand_dims %0 {axis = 0 : i32} : (tensor<16xi32>) -> tensor<1x16xi32>
    %8 = tt.broadcast %6 : (tensor<16x1x!tt.ptr<f16>>) -> tensor<16x16x!tt.ptr<f16>>
    %9 = tt.broadcast %7 : (tensor<1x16xi32>) -> tensor<16x16xi32>
    %10 = tt.addptr %8, %9 : tensor<16x16x!tt.ptr<f16>>
    %11 = tt.splat %arg4 : (i32) -> tensor<16x1xi32>
    %12 = arith.muli %2, %11 : tensor<16x1xi32>
    %13 = tt.splat %arg1 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>>
    %14 = tt.addptr %13, %12 : tensor<16x1x!tt.ptr<f16>>
    %15 = tt.expand_dims %1 {axis = 0 : i32} : (tensor<8xi32>) -> tensor<1x8xi32>
    %16 = tt.broadcast %14 : (tensor<16x1x!tt.ptr<f16>>) -> tensor<16x8x!tt.ptr<f16>>
    %17 = tt.broadcast %15 : (tensor<1x8xi32>) -> tensor<16x8xi32>
    %18 = tt.addptr %16, %17 : tensor<16x8x!tt.ptr<f16>>
    %19:3 = scf.for %arg6 = %c0 to %c64 step %c16 iter_args(%arg7 = %cst, %arg8 = %10, %arg9 = %18) -> (tensor<16x8xf32>, tensor<16x16x!tt.ptr<f16>>, tensor<16x8x!tt.ptr<f16>>) {
      %26 = tt.load %arg8 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16xf16>
      %27 = tt.load %arg9 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8xf16>
      %28 = tt.dot %26, %27, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16> * tensor<16x8xf16> -> tensor<16x8xf32>
      %29 = tt.addptr %arg8, %cst_0 : tensor<16x16x!tt.ptr<f16>>
      %30 = arith.muli %arg4, %c16_i32 : i32
      %31 = tt.splat %30 : (i32) -> tensor<16x8xi32>
      %32 = tt.addptr %arg9, %31 : tensor<16x8x!tt.ptr<f16>>
      scf.yield %28, %29, %32 : tensor<16x8xf32>, tensor<16x16x!tt.ptr<f16>>, tensor<16x8x!tt.ptr<f16>>
    }
    %20 = tt.splat %arg5 : (i32) -> tensor<16x1xi32>
    %21 = arith.muli %2, %20 : tensor<16x1xi32>
    %22 = tt.splat %arg2 : (!tt.ptr<f32>) -> tensor<16x1x!tt.ptr<f32>>
    %23 = tt.addptr %22, %21 : tensor<16x1x!tt.ptr<f32>>
    %24 = tt.broadcast %23 : (tensor<16x1x!tt.ptr<f32>>) -> tensor<16x8x!tt.ptr<f32>>
    %25 = tt.addptr %24, %17 : tensor<16x8x!tt.ptr<f32>>
    tt.store %25, %19#0 : tensor<16x8xf32>
    return
  }

IR Before LoopInvariantCodeMotion

  func public @matmul_kernel_0d1d2d3d4c56c78c(%arg0: !tt.ptr<f16> {tt.divisibility = 16 : i32}, %arg1: !tt.ptr<f16> {tt.divisibility = 16 : i32}, %arg2: !tt.ptr<f32> {tt.divisibility = 16 : i32}, %arg3: i32 {tt.divisibility = 16 : i32}, %arg4: i32, %arg5: i32) {
    %cst = arith.constant dense<0.000000e+00> : tensor<16x8xf32>
    %c0 = arith.constant 0 : index
    %c64 = arith.constant 64 : index
    %c16 = arith.constant 16 : index
    %cst_0 = arith.constant dense<16> : tensor<16x16xi32>
    %c16_i32 = arith.constant 16 : i32
    %0 = tt.make_range {end = 16 : i32, start = 0 : i32} : tensor<16xi32>
    %1 = tt.make_range {end = 8 : i32, start = 0 : i32} : tensor<8xi32>
    %2 = tt.expand_dims %0 {axis = 1 : i32} : (tensor<16xi32>) -> tensor<16x1xi32>
    %3 = tt.splat %arg3 : (i32) -> tensor<16x1xi32>
    %4 = arith.muli %2, %3 : tensor<16x1xi32>
    %5 = tt.splat %arg0 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>>
    %6 = tt.addptr %5, %4 : tensor<16x1x!tt.ptr<f16>>
    %7 = tt.expand_dims %0 {axis = 0 : i32} : (tensor<16xi32>) -> tensor<1x16xi32>
    %8 = tt.broadcast %6 : (tensor<16x1x!tt.ptr<f16>>) -> tensor<16x16x!tt.ptr<f16>>
    %9 = tt.broadcast %7 : (tensor<1x16xi32>) -> tensor<16x16xi32>
    %10 = tt.addptr %8, %9 : tensor<16x16x!tt.ptr<f16>>
    %11 = tt.splat %arg4 : (i32) -> tensor<16x1xi32>
    %12 = arith.muli %2, %11 : tensor<16x1xi32>
    %13 = tt.splat %arg1 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>>
    %14 = tt.addptr %13, %12 : tensor<16x1x!tt.ptr<f16>>
    %15 = tt.expand_dims %1 {axis = 0 : i32} : (tensor<8xi32>) -> tensor<1x8xi32>
    %16 = tt.broadcast %14 : (tensor<16x1x!tt.ptr<f16>>) -> tensor<16x8x!tt.ptr<f16>>
    %17 = tt.broadcast %15 : (tensor<1x8xi32>) -> tensor<16x8xi32>
    %18 = tt.addptr %16, %17 : tensor<16x8x!tt.ptr<f16>>
    %19:3 = scf.for %arg6 = %c0 to %c64 step %c16 iter_args(%arg7 = %cst, %arg8 = %10, %arg9 = %18) -> (tensor<16x8xf32>, tensor<16x16x!tt.ptr<f16>>, tensor<16x8x!tt.ptr<f16>>) {
      %26 = tt.load %arg8 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16xf16>
      %27 = tt.load %arg9 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8xf16>
      %28 = tt.dot %26, %27, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16> * tensor<16x8xf16> -> tensor<16x8xf32>
      %29 = tt.addptr %arg8, %cst_0 : tensor<16x16x!tt.ptr<f16>>
      %30 = arith.muli %arg4, %c16_i32 : i32
      %31 = tt.splat %30 : (i32) -> tensor<16x8xi32>
      %32 = tt.addptr %arg9, %31 : tensor<16x8x!tt.ptr<f16>>
      scf.yield %28, %29, %32 : tensor<16x8xf32>, tensor<16x16x!tt.ptr<f16>>, tensor<16x8x!tt.ptr<f16>>
    }
    %20 = tt.splat %arg5 : (i32) -> tensor<16x1xi32>
    %21 = arith.muli %2, %20 : tensor<16x1xi32>
    %22 = tt.splat %arg2 : (!tt.ptr<f32>) -> tensor<16x1x!tt.ptr<f32>>
    %23 = tt.addptr %22, %21 : tensor<16x1x!tt.ptr<f32>>
    %24 = tt.broadcast %23 : (tensor<16x1x!tt.ptr<f32>>) -> tensor<16x8x!tt.ptr<f32>>
    %25 = tt.addptr %24, %17 : tensor<16x8x!tt.ptr<f32>>
    tt.store %25, %19#0 : tensor<16x8xf32>
    return
  }

可以看到

      %30 = arith.muli %arg4, %c16_i32 : i32
      %31 = tt.splat %30 : (i32) -> tensor<16x8xi32>

这段计算的输入分别是 function argument 和 constant，不依赖 forloop 内的变量，理论上可以挪出去。

IR After LoopInvariantCodeMotion

LoopInvariantCodeMotion 是 MLIR 社区的一个 Pass，用于将无关 variable 计算挪到 forloop 外面，可以看到上小节里面的计算已经挪出去了。

  func public @matmul_kernel_0d1d2d3d4c56c78c(%arg0: !tt.ptr<f16>, %arg1: !tt.ptr<f16>, %arg2: !tt.ptr<f32>, %arg3: i32, %arg4: i32, %arg5: i32) {
    %cst = arith.constant dense<0.000000e+00> : tensor<16x8xf32>
    %c0 = arith.constant 0 : index
    %c64 = arith.constant 64 : index
    %c16 = arith.constant 16 : index
    %cst_0 = arith.constant dense<16> : tensor<16x16xi32>
    %c16_i32 = arith.constant 16 : i32
    %0 = tt.make_range {end = 16 : i32, start = 0 : i32} : tensor<16xi32>
    %1 = tt.make_range {end = 8 : i32, start = 0 : i32} : tensor<8xi32>
    %2 = tt.expand_dims %0 {axis = 1 : i32} : (tensor<16xi32>) -> tensor<16x1xi32>
    %3 = tt.splat %arg3 : (i32) -> tensor<16x1xi32>
    %4 = arith.muli %2, %3 : tensor<16x1xi32>
    %5 = tt.splat %arg0 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>>
    %6 = tt.addptr %5, %4 : tensor<16x1x!tt.ptr<f16>>
    %7 = tt.expand_dims %0 {axis = 0 : i32} : (tensor<16xi32>) -> tensor<1x16xi32>
    %8 = tt.broadcast %6 : (tensor<16x1x!tt.ptr<f16>>) -> tensor<16x16x!tt.ptr<f16>>
    %9 = tt.broadcast %7 : (tensor<1x16xi32>) -> tensor<16x16xi32>
    %10 = tt.addptr %8, %9 : tensor<16x16x!tt.ptr<f16>>
    %11 = tt.splat %arg4 : (i32) -> tensor<16x1xi32>
    %12 = arith.muli %2, %11 : tensor<16x1xi32>
    %13 = tt.splat %arg1 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>>
    %14 = tt.addptr %13, %12 : tensor<16x1x!tt.ptr<f16>>
    %15 = tt.expand_dims %1 {axis = 0 : i32} : (tensor<8xi32>) -> tensor<1x8xi32>
    %16 = tt.broadcast %14 : (tensor<16x1x!tt.ptr<f16>>) -> tensor<16x8x!tt.ptr<f16>>
    %17 = tt.broadcast %15 : (tensor<1x8xi32>) -> tensor<16x8xi32>
    %18 = tt.addptr %16, %17 : tensor<16x8x!tt.ptr<f16>>
    %19 = arith.muli %arg4, %c16_i32 : i32
    %20 = tt.splat %19 : (i32) -> tensor<16x8xi32>
    %21:3 = scf.for %arg6 = %c0 to %c64 step %c16 iter_args(%arg7 = %cst, %arg8 = %10, %arg9 = %18) -> (tensor<16x8xf32>, tensor<16x16x!tt.ptr<f16>>, tensor<16x8x!tt.ptr<f16>>) {
      %28 = tt.load %arg8 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16xf16>
      %29 = tt.load %arg9 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8xf16>
      %30 = tt.dot %28, %29, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16> * tensor<16x8xf16> -> tensor<16x8xf32>
      %31 = tt.addptr %arg8, %cst_0 : tensor<16x16x!tt.ptr<f16>>
      %32 = tt.addptr %arg9, %20 : tensor<16x8x!tt.ptr<f16>>
      scf.yield %30, %31, %32 : tensor<16x8xf32>, tensor<16x16x!tt.ptr<f16>>, tensor<16x8x!tt.ptr<f16>>
    }
    %22 = tt.splat %arg5 : (i32) -> tensor<16x1xi32>
    %23 = arith.muli %2, %22 : tensor<16x1xi32>
    %24 = tt.splat %arg2 : (!tt.ptr<f32>) -> tensor<16x1x!tt.ptr<f32>>
    %25 = tt.addptr %24, %23 : tensor<16x1x!tt.ptr<f32>>
    %26 = tt.broadcast %25 : (tensor<16x1x!tt.ptr<f32>>) -> tensor<16x8x!tt.ptr<f32>>
    %27 = tt.addptr %26, %17 : tensor<16x8x!tt.ptr<f32>>
    tt.store %27, %21#0 : tensor<16x8xf32>
    return
  }

IR After ConvertTritonToTritonGPU

这一步是在原有的硬件无关的 Triton IR 基础上加入了 GPU 相关的 data layout 和 operation.

#blocked0 = #triton_gpu.blocked<{sizePerThread = [1], threadsPerWarp = [16], warpsPerCTA = [1], order = [0]}>
#blocked1 = #triton_gpu.blocked<{sizePerThread = [1], threadsPerWarp = [8], warpsPerCTA = [1], order = [0]}>
#blocked2 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [16, 1], warpsPerCTA = [1, 1], order = [0, 1]}>
#blocked3 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [1, 16], warpsPerCTA = [1, 1], order = [0, 1]}>
#blocked4 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [16, 2], warpsPerCTA = [1, 1], order = [0, 1]}>
#blocked5 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [1, 8], warpsPerCTA = [1, 1], order = [0, 1]}>
module attributes {"triton_gpu.num-warps" = 1 : i32} {
  func public @matmul_kernel_0d1d2d3d4c56c78c(%arg0: !tt.ptr<f16>, %arg1: !tt.ptr<f16>, %arg2: !tt.ptr<f32>, %arg3: i32, %arg4: i32, %arg5: i32) {
    %cst = arith.constant dense<0.000000e+00> : tensor<16x8xf32, |\colorbox{yellow}{\strut #blocked4}|>
    %c0 = arith.constant 0 : index
    %c64 = arith.constant 64 : index
    %c16 = arith.constant 16 : index
    %cst_0 = arith.constant dense<16> : tensor<16x16xi32, #blocked4>
    %c16_i32 = arith.constant 16 : i32
    %0 = tt.make_range {end = 16 : i32, start = 0 : i32} : tensor<16xi32, #blocked0>
    %1 = tt.make_range {end = 8 : i32, start = 0 : i32} : tensor<8xi32, #blocked1>
    %2 = triton_gpu.convert_layout %0 : (tensor<16xi32, #blocked0>) -> tensor<16xi32, #triton_gpu.slice<{dim = 1, parent = #blocked2}>>
    %3 = tt.expand_dims %2 {axis = 1 : i32} : (tensor<16xi32, #triton_gpu.slice<{dim = 1, parent = #blocked2}>>) -> tensor<16x1xi32, #blocked2>
    %4 = tt.splat %arg3 : (i32) -> tensor<16x1xi32, #blocked2>
    %5 = arith.muli %3, %4 : tensor<16x1xi32, #blocked2>
    %6 = tt.splat %arg0 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>, #blocked2>
    %7 = tt.addptr %6, %5 : tensor<16x1x!tt.ptr<f16>, #blocked2>
    %8 = triton_gpu.convert_layout %0 : (tensor<16xi32, #blocked0>) -> tensor<16xi32, #triton_gpu.slice<{dim = 0, parent = #blocked3}>>
    %9 = tt.expand_dims %8 {axis = 0 : i32} : (tensor<16xi32, #triton_gpu.slice<{dim = 0, parent = #blocked3}>>) -> tensor<1x16xi32, #blocked3>
    %10 = tt.broadcast %7 : (tensor<16x1x!tt.ptr<f16>, #blocked2>) -> tensor<16x16x!tt.ptr<f16>, #blocked2>
    %11 = triton_gpu.convert_layout %10 : (tensor<16x16x!tt.ptr<f16>, #blocked2>) -> tensor<16x16x!tt.ptr<f16>, #blocked4>
    %12 = tt.broadcast %9 : (tensor<1x16xi32, #blocked3>) -> tensor<16x16xi32, #blocked3>
    %13 = triton_gpu.convert_layout %12 : (tensor<16x16xi32, #blocked3>) -> tensor<16x16xi32, #blocked4>
    %14 = tt.addptr %11, %13 : tensor<16x16x!tt.ptr<f16>, #blocked4>
    %15 = tt.splat %arg4 : (i32) -> tensor<16x1xi32, #blocked2>
    %16 = arith.muli %3, %15 : tensor<16x1xi32, #blocked2>
    %17 = tt.splat %arg1 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>, #blocked2>
    %18 = tt.addptr %17, %16 : tensor<16x1x!tt.ptr<f16>, #blocked2>
    %19 = triton_gpu.convert_layout %1 : (tensor<8xi32, #blocked1>) -> tensor<8xi32, #triton_gpu.slice<{dim = 0, parent = #blocked5}>>
    %20 = tt.expand_dims %19 {axis = 0 : i32} : (tensor<8xi32, #triton_gpu.slice<{dim = 0, parent = #blocked5}>>) -> tensor<1x8xi32, #blocked5>
    %21 = tt.broadcast %18 : (tensor<16x1x!tt.ptr<f16>, #blocked2>) -> tensor<16x8x!tt.ptr<f16>, #blocked2>
    %22 = triton_gpu.convert_layout %21 : (tensor<16x8x!tt.ptr<f16>, #blocked2>) -> tensor<16x8x!tt.ptr<f16>, #blocked4>
    %23 = tt.broadcast %20 : (tensor<1x8xi32, #blocked5>) -> tensor<16x8xi32, #blocked5>
    %24 = triton_gpu.convert_layout %23 : (tensor<16x8xi32, #blocked5>) -> tensor<16x8xi32, #blocked4>
    %25 = tt.addptr %22, %24 : tensor<16x8x!tt.ptr<f16>, #blocked4>
    %26 = arith.muli %arg4, %c16_i32 : i32
    %27 = tt.splat %26 : (i32) -> tensor<16x8xi32, #blocked4>
    %28:3 = scf.for %arg6 = %c0 to %c64 step %c16 iter_args(%arg7 = %cst, %arg8 = %14, %arg9 = %25) -> (tensor<16x8xf32, #blocked4>, tensor<16x16x!tt.ptr<f16>, #blocked4>, tensor<16x8x!tt.ptr<f16>, #blocked4>) {
      %36 = tt.load %arg8 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16xf16, #blocked4>
      %37 = tt.load %arg9 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8xf16, #blocked4>
      %38 = triton_gpu.convert_layout %36 : (tensor<16x16xf16, #blocked4>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #blocked4}>>
      %39 = triton_gpu.convert_layout %37 : (tensor<16x8xf16, #blocked4>) -> tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #blocked4}>>
      %40 = tt.dot %38, %39, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #blocked4}>> * tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #blocked4}>> -> tensor<16x8xf32, #blocked4>
      %41 = tt.addptr %arg8, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked4>
      %42 = tt.addptr %arg9, %27 : tensor<16x8x!tt.ptr<f16>, #blocked4>
      scf.yield %40, %41, %42 : tensor<16x8xf32, #blocked4>, tensor<16x16x!tt.ptr<f16>, #blocked4>, tensor<16x8x!tt.ptr<f16>, #blocked4>
    }
    %29 = tt.splat %arg5 : (i32) -> tensor<16x1xi32, #blocked2>
    %30 = arith.muli %3, %29 : tensor<16x1xi32, #blocked2>
    %31 = tt.splat %arg2 : (!tt.ptr<f32>) -> tensor<16x1x!tt.ptr<f32>, #blocked2>
    %32 = tt.addptr %31, %30 : tensor<16x1x!tt.ptr<f32>, #blocked2>
    %33 = tt.broadcast %32 : (tensor<16x1x!tt.ptr<f32>, #blocked2>) -> tensor<16x8x!tt.ptr<f32>, #blocked2>
    %34 = triton_gpu.convert_layout %33 : (tensor<16x8x!tt.ptr<f32>, #blocked2>) -> tensor<16x8x!tt.ptr<f32>, #blocked4>
    %35 = tt.addptr %34, %24 : tensor<16x8x!tt.ptr<f32>, #blocked4>
    tt.store %35, %28#0 : tensor<16x8xf32, #blocked4>
    return
  }

这里比较明显的是

作为 dotOp 的输出， %40 应该是 mma layout，但这一步还是 blocked layout，这个会在下一节里面改写
%38, %39 这些的 layout 应该是 dot_op<mma> 但由于 mma layout 还没有给定，所以还是 dot_op<blocked>

IR After TritonGPUCombineOps

这一步会包含很多 Op pattern 的改写，直接的变化是

给 dot 相关的增加了 mma 的 data layout
插入了 mma layout 相关的 convert_layout

#blocked0 = #triton_gpu.blocked<{sizePerThread = [1, 8], threadsPerWarp = [16, 2], warpsPerCTA = [1, 1], order = [1, 0]}>
#blocked1 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [4, 8], warpsPerCTA = [1, 1], order = [1, 0]}>
#mma = #triton_gpu.mma<{version = 2, warpsPerCTA = [1, 1]}>
module attributes {"triton_gpu.num-warps" = 1 : i32} {
  func public @matmul_kernel_0d1d2d3d4c56c78c(%arg0: !tt.ptr<f16> {tt.divisibility = 16 : i32}, %arg1: !tt.ptr<f16> {tt.divisibility = 16 : i32}, %arg2: !tt.ptr<f32> {tt.divisibility = 16 : i32}, %arg3: i32 {tt.divisibility = 16 : i32}, %arg4: i32, %arg5: i32) {
    %c0 = arith.constant 0 : index
    %c64 = arith.constant 64 : index
    %c16 = arith.constant 16 : index
    %c16_i32 = arith.constant 16 : i32
    %cst = arith.constant dense<0.000000e+00> : tensor<16x8xf32, #mma>
    %cst_0 = arith.constant dense<16> : tensor<16x16xi32, #blocked0>
    %0 = tt.make_range {end = 16 : i32, start = 0 : i32} : tensor<16xi32, #triton_gpu.slice<{dim = 1, parent = #blocked0}>>
    %1 = tt.make_range {end = 16 : i32, start = 0 : i32} : tensor<16xi32, #triton_gpu.slice<{dim = 1, parent = #blocked1}>>
    %2 = tt.make_range {end = 16 : i32, start = 0 : i32} : tensor<16xi32, #triton_gpu.slice<{dim = 1, parent = #blocked1}>>
    %3 = tt.splat %arg3 : (i32) -> tensor<16x1xi32, #blocked0>
    %4 = tt.splat %arg0 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>, #blocked0>
    %5 = tt.make_range {end = 16 : i32, start = 0 : i32} : tensor<16xi32, #triton_gpu.slice<{dim = 0, parent = #blocked0}>>
    %6 = tt.expand_dims %0 {axis = 1 : i32} : (tensor<16xi32, #triton_gpu.slice<{dim = 1, parent = #blocked0}>>) -> tensor<16x1xi32, #blocked0>
    %7 = arith.muli %6, %3 : tensor<16x1xi32, #blocked0>
    %8 = tt.addptr %4, %7 : tensor<16x1x!tt.ptr<f16>, #blocked0>
    %9 = tt.broadcast %8 : (tensor<16x1x!tt.ptr<f16>, #blocked0>) -> tensor<16x16x!tt.ptr<f16>, #blocked0>
    %10 = tt.expand_dims %5 {axis = 0 : i32} : (tensor<16xi32, #triton_gpu.slice<{dim = 0, parent = #blocked0}>>) -> tensor<1x16xi32, #blocked0>
    %11 = tt.broadcast %10 : (tensor<1x16xi32, #blocked0>) -> tensor<16x16xi32, #blocked0>
    %12 = tt.splat %arg4 : (i32) -> tensor<16x1xi32, #blocked1>
    %13 = tt.splat %arg1 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>, #blocked1>
    %14 = tt.make_range {end = 8 : i32, start = 0 : i32} : tensor<8xi32, #triton_gpu.slice<{dim = 0, parent = #blocked1}>>
    %15 = tt.make_range {end = 8 : i32, start = 0 : i32} : tensor<8xi32, #triton_gpu.slice<{dim = 0, parent = #blocked1}>>
    %16 = tt.expand_dims %1 {axis = 1 : i32} : (tensor<16xi32, #triton_gpu.slice<{dim = 1, parent = #blocked1}>>) -> tensor<16x1xi32, #blocked1>
    %17 = arith.muli %16, %12 : tensor<16x1xi32, #blocked1>
    %18 = tt.addptr %13, %17 : tensor<16x1x!tt.ptr<f16>, #blocked1>
    %19 = tt.broadcast %18 : (tensor<16x1x!tt.ptr<f16>, #blocked1>) -> tensor<16x8x!tt.ptr<f16>, #blocked1>
    %20 = tt.expand_dims %14 {axis = 0 : i32} : (tensor<8xi32, #triton_gpu.slice<{dim = 0, parent = #blocked1}>>) -> tensor<1x8xi32, #blocked1>
    %21 = tt.broadcast %20 : (tensor<1x8xi32, #blocked1>) -> tensor<16x8xi32, #blocked1>
    %22 = tt.expand_dims %15 {axis = 0 : i32} : (tensor<8xi32, #triton_gpu.slice<{dim = 0, parent = #blocked1}>>) -> tensor<1x8xi32, #blocked1>
    %23 = tt.broadcast %22 : (tensor<1x8xi32, #blocked1>) -> tensor<16x8xi32, #blocked1>
    %24 = arith.muli %arg4, %c16_i32 : i32
    %25 = tt.splat %24 : (i32) -> tensor<16x8xi32, #blocked1>
    %26 = tt.addptr %9, %11 : tensor<16x16x!tt.ptr<f16>, #blocked0>
    %27 = tt.addptr %19, %21 : tensor<16x8x!tt.ptr<f16>, #blocked1>
    %28:3 = scf.for %arg6 = %c0 to %c64 step %c16 iter_args(%arg7 = %cst, %arg8 = %26, %arg9 = %27) -> (tensor<16x8xf32, #mma>, tensor<16x16x!tt.ptr<f16>, #blocked0>, tensor<16x8x!tt.ptr<f16>, #blocked1>) {
      %37 = tt.load %arg8 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16xf16, #blocked0>
      %38 = tt.load %arg9 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8xf16, #blocked1>
      %39 = triton_gpu.convert_layout %37 : (tensor<16x16xf16, #blocked0>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>
      %40 = triton_gpu.convert_layout %38 : (tensor<16x8xf16, #blocked1>) -> tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>
      %41 = tt.dot %39, %40, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>> * tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>> -> tensor<16x8xf32, #mma>
      %42 = tt.addptr %arg8, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
      %43 = tt.addptr %arg9, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
      scf.yield %41, %42, %43 : tensor<16x8xf32, #mma>, tensor<16x16x!tt.ptr<f16>, #blocked0>, tensor<16x8x!tt.ptr<f16>, #blocked1>
    }
    %29 = tt.splat %arg5 : (i32) -> tensor<16x1xi32, #blocked1>
    %30 = tt.splat %arg2 : (!tt.ptr<f32>) -> tensor<16x1x!tt.ptr<f32>, #blocked1>
    %31 = tt.expand_dims %2 {axis = 1 : i32} : (tensor<16xi32, #triton_gpu.slice<{dim = 1, parent = #blocked1}>>) -> tensor<16x1xi32, #blocked1>
    %32 = arith.muli %31, %29 : tensor<16x1xi32, #blocked1>
    %33 = tt.addptr %30, %32 : tensor<16x1x!tt.ptr<f32>, #blocked1>
    %34 = tt.broadcast %33 : (tensor<16x1x!tt.ptr<f32>, #blocked1>) -> tensor<16x8x!tt.ptr<f32>, #blocked1>
    %35 = tt.addptr %34, %23 : tensor<16x8x!tt.ptr<f32>, #blocked1>
    %36 = triton_gpu.convert_layout %28#0 : (tensor<16x8xf32, #mma>) -> tensor<16x8xf32, #blocked1>
    tt.store %35, %36 : tensor<16x8xf32, #blocked1>
    return
  }

IR After TritonGPUPipeline

这一步可以认为是在 global memory -> shared memory 的数据搬运做 Pipeline 优化。

#blocked0 = #triton_gpu.blocked<{sizePerThread = [1, 8], threadsPerWarp = [16, 2], warpsPerCTA = [1, 1], order = [1, 0]}>
#blocked1 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [4, 8], warpsPerCTA = [1, 1], order = [1, 0]}>
#mma = #triton_gpu.mma<{version = 2, warpsPerCTA = [1, 1]}>
#shared0 = #triton_gpu.shared<{vec = 8, perPhase = 4, maxPhase = 2, order = [1, 0]}>
#shared1 = #triton_gpu.shared<{vec = 8, perPhase = 8, maxPhase = 1, order = [1, 0]}>
module attributes {"triton_gpu.num-warps" = 1 : i32} {
  func public @matmul_kernel_0d1d2d3d4c56c78c(%arg0: !tt.ptr<f16>, %arg1: !tt.ptr<f16>, %arg2: !tt.ptr<f32>, %arg3: i32, %arg4: i32, %arg5: i32) {
    ...

    %28 = arith.cmpi slt, %c0, %c64 : index
    %29 = triton_gpu.alloc_tensor : tensor<3x16x16xf16, #shared0>
    %30 = tt.splat %28 : (i1) -> tensor<16x16xi1, #blocked0>
    %31 = triton_gpu.insert_slice_async %26, %29, %c0_i32, %30 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16x!tt.ptr<f16>, #blocked0> -> tensor<3x16x16xf16, #shared0>
    %32 = triton_gpu.alloc_tensor : tensor<3x16x8xf16, #shared1>
    %33 = tt.splat %28 : (i1) -> tensor<16x8xi1, #blocked1>
    %34 = triton_gpu.insert_slice_async %27, %32, %c0_i32, %33 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8x!tt.ptr<f16>, #blocked1> -> tensor<3x16x8xf16, #shared1>
    %35 = tt.addptr %26, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
    %36 = tt.addptr %27, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
    ...
    %40 = tt.splat %39 : (i1) -> tensor<16x16xi1, #blocked0>
    %41 = triton_gpu.insert_slice_async %35, %31, %37, %40 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16x!tt.ptr<f16>, #blocked0> -> tensor<3x16x16xf16, #shared0>
    %42 = tt.splat %39 : (i1) -> tensor<16x8xi1, #blocked1>
    %43 = triton_gpu.insert_slice_async %36, %34, %37, %42 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8x!tt.ptr<f16>, #blocked1> -> tensor<3x16x8xf16, #shared1>
    %44 = tt.addptr %35, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
    %45 = tt.addptr %36, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
    %c1_i32_1 = arith.constant 1 : i32
    %46 = arith.addi %37, %c1_i32_1 : i32
    triton_gpu.async_wait {num = 2 : i32}
    %c0_i32_2 = arith.constant 0 : i32
    %47 = tensor.extract_slice %41[0, 0, 0] [1, 16, 16] [1, 1, 1] : tensor<3x16x16xf16, #shared0> to tensor<16x16xf16, #shared0>
    %48 = tensor.extract_slice %43[0, 0, 0] [1, 16, 8] [1, 1, 1] : tensor<3x16x8xf16, #shared1> to tensor<16x8xf16, #shared1>
    %c1_i32_3 = arith.constant 1 : i32
    %49 = arith.addi %c0_i32_2, %c1_i32_3 : i32
    %50:12 = scf.for %arg6 = %c0 to %c64 step %c16 iter_args(%arg7 = %cst, %arg8 = %26, %arg9 = %27, %arg10 = %41, %arg11 = %43, %arg12 = %47, %arg13 = %48, %arg14 = %45, %arg15 = %44, %arg16 = %38, %arg17 = %46, %arg18 = %49) -> (tensor<16x8xf32, #mma>, tensor<16x16x!tt.ptr<f16>, #blocked0>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<3x16x16xf16, #shared0>, tensor<3x16x8xf16, #shared1>, tensor<16x16xf16, #shared0>, tensor<16x8xf16, #shared1>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<16x16x!tt.ptr<f16>, #blocked0>, index, i32, i32) {
      %59 = triton_gpu.convert_layout %arg12 : (tensor<16x16xf16, #shared0>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>
      %60 = triton_gpu.convert_layout %arg13 : (tensor<16x8xf16, #shared1>) -> tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>
      %61 = tt.dot %59, %60, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>> * tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>> -> tensor<16x8xf32, #mma>
      %62 = tt.addptr %arg8, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
      %63 = tt.addptr %arg9, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
      %64 = arith.addi %arg16, %c16 : index
      %65 = arith.cmpi slt, %64, %c64 : index
      %c3_i32 = arith.constant 3 : i32
      %66 = arith.remsi %arg17, %c3_i32 : i32
      %c3_i32_4 = arith.constant 3 : i32
      %67 = arith.remsi %arg18, %c3_i32_4 : i32
      %68 = arith.index_cast %67 : i32 to index
      %69 = tt.splat %65 : (i1) -> tensor<16x16xi1, #blocked0>
      %70 = triton_gpu.insert_slice_async %arg15, %arg10, %66, %69 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16x!tt.ptr<f16>, #blocked0> -> tensor<3x16x16xf16, #shared0>
      %71 = tt.splat %65 : (i1) -> tensor<16x8xi1, #blocked1>
      %72 = triton_gpu.insert_slice_async %arg14, %arg11, %66, %71 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8x!tt.ptr<f16>, #blocked1> -> tensor<3x16x8xf16, #shared1>
      %73 = tt.addptr %arg15, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
      %74 = tt.addptr %arg14, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
      triton_gpu.async_wait {num = 2 : i32}
      %75 = tensor.extract_slice %70[%68, 0, 0] [1, 16, 16] [1, 1, 1] : tensor<3x16x16xf16, #shared0> to tensor<16x16xf16, #shared0>
      %76 = tensor.extract_slice %72[%68, 0, 0] [1, 16, 8] [1, 1, 1] : tensor<3x16x8xf16, #shared1> to tensor<16x8xf16, #shared1>
      %c1_i32_5 = arith.constant 1 : i32
      %77 = arith.addi %arg17, %c1_i32_5 : i32
      %c1_i32_6 = arith.constant 1 : i32
      %78 = arith.addi %arg18, %c1_i32_6 : i32
      scf.yield %61, %62, %63, %70, %72, %75, %76, %74, %73, %64, %77, %78 : tensor<16x8xf32, #mma>, tensor<16x16x!tt.ptr<f16>, #blocked0>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<3x16x16xf16, #shared0>, tensor<3x16x8xf16, #shared1>, tensor<16x16xf16, #shared0>, tensor<16x8xf16, #shared1>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<16x16x!tt.ptr<f16>, #blocked0>, index, i32, i32
    }
    ...
    return
  }
}

IR Before TritonGPUPrefetch

#blocked0 = #triton_gpu.blocked<{sizePerThread = [1, 8], threadsPerWarp = [16, 2], warpsPerCTA = [1, 1], order = [1, 0]}>
#blocked1 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [4, 8], warpsPerCTA = [1, 1], order = [1, 0]}>
#mma = #triton_gpu.mma<{version = 2, warpsPerCTA = [1, 1]}>
#shared0 = #triton_gpu.shared<{vec = 8, perPhase = 4, maxPhase = 2, order = [1, 0]}>
#shared1 = #triton_gpu.shared<{vec = 8, perPhase = 8, maxPhase = 1, order = [1, 0]}>
module attributes {"triton_gpu.num-warps" = 1 : i32} {
  func public @matmul_kernel_0d1d2d3d4c56c78c(%arg0: !tt.ptr<f16>, %arg1: !tt.ptr<f16>, %arg2: !tt.ptr<f32>, %arg3: i32, %arg4: i32, %arg5: i32) {
    ...

    %28 = arith.cmpi slt, %c0, %c64 : index
    %29 = triton_gpu.alloc_tensor : tensor<3x16x16xf16, #shared0>
    %30 = tt.splat %28 : (i1) -> tensor<16x16xi1, #blocked0>
    %31 = triton_gpu.insert_slice_async %26, %29, %c0_i32, %30 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16x!tt.ptr<f16>, #blocked0> -> tensor<3x16x16xf16, #shared0>
    %32 = triton_gpu.alloc_tensor : tensor<3x16x8xf16, #shared1>
    %33 = tt.splat %28 : (i1) -> tensor<16x8xi1, #blocked1>
    %34 = triton_gpu.insert_slice_async %27, %32, %c0_i32, %33 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8x!tt.ptr<f16>, #blocked1> -> tensor<3x16x8xf16, #shared1>
    %35 = tt.addptr %26, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
    %36 = tt.addptr %27, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
    ...
    %40 = tt.splat %39 : (i1) -> tensor<16x16xi1, #blocked0>
    %41 = triton_gpu.insert_slice_async %35, %31, %37, %40 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16x!tt.ptr<f16>, #blocked0> -> tensor<3x16x16xf16, #shared0>
    %42 = tt.splat %39 : (i1) -> tensor<16x8xi1, #blocked1>
    %43 = triton_gpu.insert_slice_async %36, %34, %37, %42 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8x!tt.ptr<f16>, #blocked1> -> tensor<3x16x8xf16, #shared1>
    %44 = tt.addptr %35, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
    %45 = tt.addptr %36, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
    %c1_i32_1 = arith.constant 1 : i32
    %46 = arith.addi %37, %c1_i32_1 : i32
    triton_gpu.async_wait {num = 2 : i32}
    %c0_i32_2 = arith.constant 0 : i32
    %47 = tensor.extract_slice %41[0, 0, 0] [1, 16, 16] [1, 1, 1] : tensor<3x16x16xf16, #shared0> to tensor<16x16xf16, #shared0>
    %48 = tensor.extract_slice %43[0, 0, 0] [1, 16, 8] [1, 1, 1] : tensor<3x16x8xf16, #shared1> to tensor<16x8xf16, #shared1>
    %c1_i32_3 = arith.constant 1 : i32
    %49 = arith.addi %c0_i32_2, %c1_i32_3 : i32
    %50:12 = scf.for %arg6 = %c0 to %c64 step %c16 iter_args(%arg7 = %cst, %arg8 = %26, %arg9 = %27, %arg10 = %41, %arg11 = %43, %arg12 = %47, %arg13 = %48, %arg14 = %45, %arg15 = %44, %arg16 = %38, %arg17 = %46, %arg18 = %49) -> (tensor<16x8xf32, #mma>, tensor<16x16x!tt.ptr<f16>, #blocked0>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<3x16x16xf16, #shared0>, tensor<3x16x8xf16, #shared1>, tensor<16x16xf16, #shared0>, tensor<16x8xf16, #shared1>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<16x16x!tt.ptr<f16>, #blocked0>, index, i32, i32) {
      %59 = triton_gpu.convert_layout %arg12 : (tensor<16x16xf16, #shared0>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>
      %60 = triton_gpu.convert_layout %arg13 : (tensor<16x8xf16, #shared1>) -> tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>
      %61 = tt.dot %59, %60, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>> * tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>> -> tensor<16x8xf32, #mma>
      %62 = tt.addptr %arg8, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
      %63 = tt.addptr %arg9, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
      %64 = arith.addi %arg16, %c16 : index
      %65 = arith.cmpi slt, %64, %c64 : index
      %c3_i32 = arith.constant 3 : i32
      %66 = arith.remsi %arg17, %c3_i32 : i32
      %c3_i32_4 = arith.constant 3 : i32
      %67 = arith.remsi %arg18, %c3_i32_4 : i32
      %68 = arith.index_cast %67 : i32 to index
      %69 = tt.splat %65 : (i1) -> tensor<16x16xi1, #blocked0>
      %70 = triton_gpu.insert_slice_async %arg15, %arg10, %66, %69 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16x!tt.ptr<f16>, #blocked0> -> tensor<3x16x16xf16, #shared0>
      %71 = tt.splat %65 : (i1) -> tensor<16x8xi1, #blocked1>
      %72 = triton_gpu.insert_slice_async %arg14, %arg11, %66, %71 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8x!tt.ptr<f16>, #blocked1> -> tensor<3x16x8xf16, #shared1>
      %73 = tt.addptr %arg15, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
      %74 = tt.addptr %arg14, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
      triton_gpu.async_wait {num = 2 : i32}
      %75 = tensor.extract_slice %70[%68, 0, 0] [1, 16, 16] [1, 1, 1] : tensor<3x16x16xf16, #shared0> to tensor<16x16xf16, #shared0>
      %76 = tensor.extract_slice %72[%68, 0, 0] [1, 16, 8] [1, 1, 1] : tensor<3x16x8xf16, #shared1> to tensor<16x8xf16, #shared1>
      %c1_i32_5 = arith.constant 1 : i32
      %77 = arith.addi %arg17, %c1_i32_5 : i32
      %c1_i32_6 = arith.constant 1 : i32
      %78 = arith.addi %arg18, %c1_i32_6 : i32
      scf.yield %61, %62, %63, %70, %72, %75, %76, %74, %73, %64, %77, %78 : tensor<16x8xf32, #mma>, tensor<16x16x!tt.ptr<f16>, #blocked0>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<3x16x16xf16, #shared0>, tensor<3x16x8xf16, #shared1>, tensor<16x16xf16, #shared0>, tensor<16x8xf16, #shared1>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<16x16x!tt.ptr<f16>, #blocked0>, index, i32, i32
    }
    ...
    return
  }
}

IR After TritonGPUPrefetch

这一步可以认为是在 Dot 相关的 shared memory -> registers 的数据搬运阶段做 Pipepline 优化。

#blocked0 = #triton_gpu.blocked<{sizePerThread = [1, 8], threadsPerWarp = [16, 2], warpsPerCTA = [1, 1], order = [1, 0]}>
#blocked1 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [4, 8], warpsPerCTA = [1, 1], order = [1, 0]}>
#mma = #triton_gpu.mma<{version = 2, warpsPerCTA = [1, 1]}>
#shared0 = #triton_gpu.shared<{vec = 8, perPhase = 4, maxPhase = 2, order = [1, 0]}>
#shared1 = #triton_gpu.shared<{vec = 8, perPhase = 8, maxPhase = 1, order = [1, 0]}>
module attributes {"triton_gpu.num-warps" = 1 : i32} {
  func public @matmul_kernel_0d1d2d3d4c56c78c(%arg0: !tt.ptr<f16> {tt.divisibility = 16 : i32}, %arg1: !tt.ptr<f16> {tt.divisibility = 16 : i32}, %arg2: !tt.ptr<f32> {tt.divisibility = 16 : i32}, %arg3: i32 {tt.divisibility = 16 : i32}, %arg4: i32, %arg5: i32) {
    ...
    triton_gpu.async_wait {num = 2 : i32}
    %c0_i32_2 = arith.constant 0 : i32
    %47 = tensor.extract_slice %41[0, 0, 0] [1, 16, 16] [1, 1, 1] : tensor<3x16x16xf16, #shared0> to tensor<16x16xf16, #shared0>
    %48 = tensor.extract_slice %43[0, 0, 0] [1, 16, 8] [1, 1, 1] : tensor<3x16x8xf16, #shared1> to tensor<16x8xf16, #shared1>
    %c1_i32_3 = arith.constant 1 : i32
    %49 = arith.addi %c0_i32_2, %c1_i32_3 : i32
    %50 = tensor.extract_slice %47[0, 0] [16, 16] [1, 1] : tensor<16x16xf16, #shared0> to tensor<16x16xf16, #shared0>
    %51 = triton_gpu.convert_layout %50 : (tensor<16x16xf16, #shared0>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>
    %52 = tensor.extract_slice %48[0, 0] [16, 8] [1, 1] : tensor<16x8xf16, #shared1> to tensor<16x8xf16, #shared1>
    %53 = triton_gpu.convert_layout %52 : (tensor<16x8xf16, #shared1>) -> tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>
    %54:14 = scf.for %arg6 = %c0 to %c64 step %c16 iter_args(%arg7 = %cst, %arg8 = %26, %arg9 = %27, %arg10 = %41, %arg11 = %43, %arg12 = %47, %arg13 = %48, %arg14 = %45, %arg15 = %44, %arg16 = %38, %arg17 = %46, %arg18 = %49, %arg19 = %51, %arg20 = %53) -> (tensor<16x8xf32, #mma>, tensor<16x16x!tt.ptr<f16>, #blocked0>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<3x16x16xf16, #shared0>, tensor<3x16x8xf16, #shared1>, tensor<16x16xf16, #shared0>, tensor<16x8xf16, #shared1>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<16x16x!tt.ptr<f16>, #blocked0>, index, i32, i32, tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>, tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>) {
      %63 = triton_gpu.convert_layout %arg12 : (tensor<16x16xf16, #shared0>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>
      %64 = triton_gpu.convert_layout %arg13 : (tensor<16x8xf16, #shared1>) -> tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>
      %65 = tt.dot %63, %64, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>> * tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>> -> tensor<16x8xf32, #mma>
      %66 = tt.dot %arg19, %arg20, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>> * tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>> -> tensor<16x8xf32, #mma>
      %67 = tt.addptr %arg8, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
      %68 = tt.addptr %arg9, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
      %69 = arith.addi %arg16, %c16 : index
      %70 = arith.cmpi slt, %69, %c64 : index
      %c3_i32 = arith.constant 3 : i32
      %71 = arith.remsi %arg17, %c3_i32 : i32
      %c3_i32_4 = arith.constant 3 : i32
      %72 = arith.remsi %arg18, %c3_i32_4 : i32
      %73 = arith.index_cast %72 : i32 to index
      %74 = tt.splat %70 : (i1) -> tensor<16x16xi1, #blocked0>
      %75 = triton_gpu.insert_slice_async %arg15, %arg10, %71, %74 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16x!tt.ptr<f16>, #blocked0> -> tensor<3x16x16xf16, #shared0>
      %76 = tt.splat %70 : (i1) -> tensor<16x8xi1, #blocked1>
      %77 = triton_gpu.insert_slice_async %arg14, %arg11, %71, %76 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8x!tt.ptr<f16>, #blocked1> -> tensor<3x16x8xf16, #shared1>
      %78 = tt.addptr %arg15, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
      %79 = tt.addptr %arg14, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
      triton_gpu.async_wait {num = 2 : i32}
      %80 = tensor.extract_slice %75[%73, 0, 0] [1, 16, 16] [1, 1, 1] : tensor<3x16x16xf16, #shared0> to tensor<16x16xf16, #shared0>
      %81 = tensor.extract_slice %77[%73, 0, 0] [1, 16, 8] [1, 1, 1] : tensor<3x16x8xf16, #shared1> to tensor<16x8xf16, #shared1>
      %c1_i32_5 = arith.constant 1 : i32
      %82 = arith.addi %arg17, %c1_i32_5 : i32
      %c1_i32_6 = arith.constant 1 : i32
      %83 = arith.addi %arg18, %c1_i32_6 : i32
      %84 = tensor.extract_slice %80[0, 0] [16, 16] [1, 1] : tensor<16x16xf16, #shared0> to tensor<16x16xf16, #shared0>
      %85 = triton_gpu.convert_layout %84 : (tensor<16x16xf16, #shared0>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>
      %86 = tensor.extract_slice %81[0, 0] [16, 8] [1, 1] : tensor<16x8xf16, #shared1> to tensor<16x8xf16, #shared1>
      %87 = triton_gpu.convert_layout %86 : (tensor<16x8xf16, #shared1>) -> tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>
      scf.yield %65, %67, %68, %75, %77, %80, %81, %79, %78, %69, %82, %83, %85, %87 : tensor<16x8xf32, #mma>, tensor<16x16x!tt.ptr<f16>, #blocked0>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<3x16x16xf16, #shared0>, tensor<3x16x8xf16, #shared1>, tensor<16x16xf16, #shared0>, tensor<16x8xf16, #shared1>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<16x16x!tt.ptr<f16>, #blocked0>, index, i32, i32, tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>, tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>
    }
    ...
    return
  }
}

IR After TritonGPUToLLVM

MLIR 阶段的最后一步就是 translate 到 LLVM dialect，可以看到其中 Triton backend 插入的 Inline Asm。

module attributes {"triton_gpu.num-warps" = 4 : i32, triton_gpu.shared = 36864 : i32} {
  llvm.mlir.global external @global_smem() {addr_space = 3 : i32} : !llvm.array<0 x i8>
  llvm.func @matmul_kernel_0d1d2d3d4c5d6c7d8c(%arg0: !llvm.ptr<f16, 1> {tt.divisibility = 16 : i32}, %arg1: !llvm.ptr<f16, 1> {tt.divisibility = 16 : i32}, %arg2: !llvm.ptr<f32, 1> {tt.divisibility = 16 : i32}, %arg3: i32 {tt.divisibility = 16 : i32}, %arg4: i32 {tt.divisibility = 16 : i32}, %arg5: i32 {tt.divisibility = 16 : i32}) attributes {nvvm.kernel = 1 : ui1, nvvm.maxntid = 128 : i32, sym_visibility = "public"} {
    %0 = llvm.mlir.addressof @global_smem : !llvm.ptr<array<0 x i8>, 3>
    %1 = llvm.bitcast %0 : !llvm.ptr<array<0 x i8>, 3> to !llvm.ptr<i8, 3>
    %2 = llvm.mlir.constant(3 : i32) : i32
    %3 = llvm.mlir.constant(1 : i32) : i32
    %4 = llvm.mlir.constant(0 : i32) : i32
    %5 = llvm.mlir.constant(2 : i32) : i32
    %6 = llvm.mlir.constant(true) : i1
    %7 = llvm.mlir.constant(32 : index) : i32
    %8 = llvm.mlir.constant(32 : i32) : i32
    %9 = llvm.mlir.constant(0.000000e+00 : f32) : f32

    ...
    %567 = llvm.inline_asm has_side_effects asm_dialect = att operand_attrs = [] "ldmatrix.sync.aligned.m8n8.x4.shared.b16 { $0, $1, $2, $3 }, [ $4 + 0 ];", "=r,=r,=r,=r,r" %566 : (!llvm.ptr<f16, 3>) -> !llvm.struct<(vector<2xf16>, vector<2xf16>, vector<2xf16>, vector<2xf16>)>

    ...
    %765 = llvm.inline_asm has_side_effects asm_dialect = att operand_attrs = [] "mma.sync.aligned.m16n8k16.row.col.f32.f16.f16.f32 { $0, $1, $2, $3 }, { $4, $5, $6, $7 }, { $8, $9 }, { $10, $11, $12, $13 };", "=r,=r,=r,=r,r,r,r,r,r,r,0,1,2,3" %677, %679, %678, %680, %685, %686, %701, %702, %703, %704 : (vector<2xf16>, vector<2xf16>, vector<2xf16>, vector<2xf16>, vector<2xf16>, vector<2xf16>, f32, f32, f32, f32) -> !llvm.struct<(f32, f32, f32, f32)>
    ...
    %1789 = llvm.inline_asm has_side_effects asm_dialect = att operand_attrs = [] "@$5 st.global.v4.b32 [ $4 + 0 ], { $0, $1, $2, $3 };", "r,r,r,r,l,b" %1782, %1784, %1786, %1788, %1449, %6 : (i32, i32, i32, i32, !llvm.ptr<f32, 1>, i1) -> !llvm.void
    ...